Show the code
data <- read.csv("data/euro-tech-money.csv")Introduction
Recently, I stumbled upon a Reddit post where someone was gathering salary data from the tech sector throughout Europe. It piqued my interest to explore how these salaries vary among various countries and positions. So, I chose to employ R for data collection and analysis.
Data Collection
Let’s start by fetching the data from the Google Sheet.
Show the code
document <- "1iTNwiAQ0s5iD6RqI7B30uWqQ8wNJqRnmHvxo5zRffu8"
sheet <- "603717461"
url = sprintf(
"https://docs.google.com/spreadsheets/d/%s/gviz/tq?tqx=out:csv&sheet=%s",
document,
sheet
)
download.file(url, destfile = "data/euro-tech-money.csv", mode = "wb")Once downloaded, we can load the data into our R environment.
The dataset consists of 572 observations in 12 columns named Job.Title, Company, City, Seniority, Pre.Tax.TC, After.Tax.TC, Yearly.Savings, Lifestyle, Household.Size, Share.of.Household.Expenses, Country, and Timestamp. See summary below.
Show summary
Job.Title Company City Seniority
Length:572 Length:572 Length:572 Length:572
Class :character Class :character Class :character Class :character
Mode :character Mode :character Mode :character Mode :character
Pre.Tax.TC After.Tax.TC Yearly.Savings Lifestyle
Min. : 13646 Min. : 10000 Min. : -2000 Length:572
1st Qu.: 48000 1st Qu.: 32600 1st Qu.: 8000 Class :character
Median : 70000 Median : 46500 Median : 17000 Mode :character
Mean : 85140 Mean : 58791 Mean : 23915
3rd Qu.: 99600 3rd Qu.: 65190 3rd Qu.: 30000
Max. :700000 Max. :1575000 Max. :270000
NA's :11 NA's :23 NA's :68
Household.Size Share.of.Household.Expenses Country
Min. :1.000 Min. : 0.0 Length:572
1st Qu.:1.000 1st Qu.: 65.0 Class :character
Median :2.000 Median :100.0 Mode :character
Mean :1.853 Mean : 82.3
3rd Qu.:2.000 3rd Qu.:100.0
Max. :7.000 Max. :100.0
NA's :22 NA's :55
Timestamp
Length:572
Class :character
Mode :character
Geography
Let’s take a look at the location of respondents. We’re going to load a map of Europe and plot the cities where the respondents are located. The map will also show the number of respondents in each city and their median salary in USD.
Show the code
library(giscoR)
library(maps)
library(dplyr)
library(stringr)
library(ggplot2)
library(ggrepel)
# Load the map of Europe
europe <- gisco_get_countries(
region = "Europe",
resolution = 1,
cache_dir = "/tmp/giscoR"
)
# Get the cities
cities <- world.cities |>
filter(str_to_upper(country.etc) %in% unique(str_to_upper(data$Country))) |>
select(name, country.etc, long, lat)
# Change case in the column to title case
data <- data |> mutate(City = str_to_title(City))
# Group responses data frame by the city
by_city <- select(data, City, Pre.Tax.TC) |>
group_by(City) |>
summarise(
resp_count = n(),
median_salary = median(Pre.Tax.TC, na.rm = TRUE)
)
# Join the cities and responses data frames
by <- join_by(name == City)
by_city <- inner_join(cities, by_city, by)
p <- by_city |>
arrange(resp_count) |>
mutate(name = factor(name, unique(name))) |>
ggplot() +
geom_sf(
data = europe,
fill = "grey",
alpha = 0.3
) +
geom_point(
aes(
x = long,
y = lat,
size = resp_count,
color = median_salary
),
alpha = 0.9
) +
scale_color_viridis_c(
trans = "log", option = "plasma",
breaks = c(25000, 50000, 100000, 200000, 400000)
) +
theme_void() +
ylim(35, 65) +
xlim(-15, 40)
p1 <- p + theme(
legend.position = "none",
plot.margin = grid::unit(c(50, 50, 50, 50), "pt")
)
ggsave("image.png", plot = p1, width = 8, height = 8)
p + geom_text_repel(
data = by_city |> arrange(resp_count) |> tail(20),
aes(x = long, y = lat, label = name),
size = 4
) +
theme(
legend.position = "right",
legend.key.height = unit(20, "pt"),
legend.box.margin = margin(0, 0, 0, 20)
)
Salaries by City
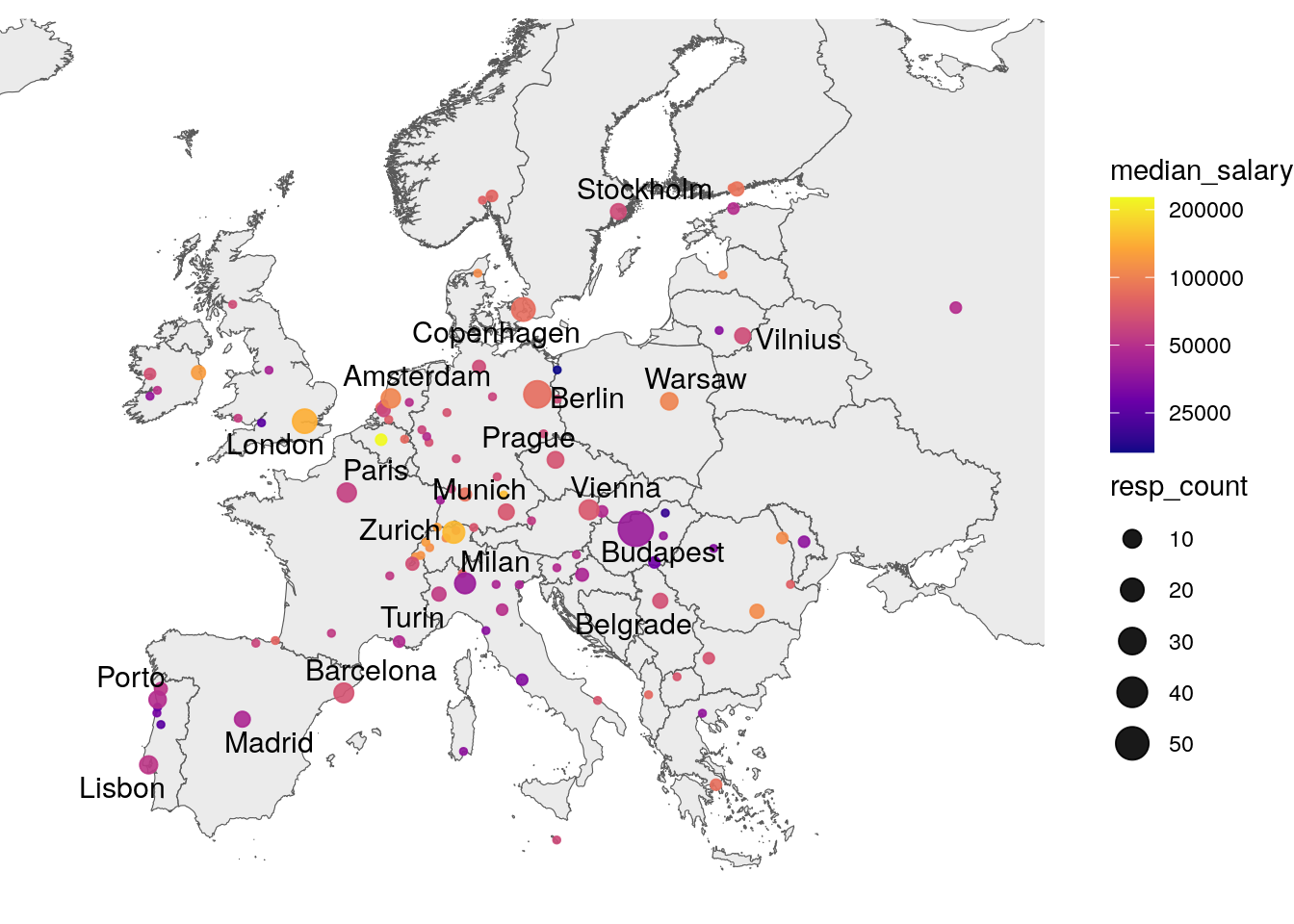
The total number of cities is 105. Below is a list of the top 10 and bottom 10 cities with at least 5 respondents, ranked by median salary. While these plots can provide a general idea of the salary distribution, it is not the best idea to compare salaries across cities directly, as the salary may vary depending on other factors like job title or seniority.
Show the code
library(scales)
cities_ranked <- data |>
inner_join(cities, by = c("City" = "name")) |>
group_by(City) |>
summarize(median_salary = median(Pre.Tax.TC), resp_count = n()) |>
filter(resp_count > 4) |>
arrange(desc(median_salary))
data <- data |>
mutate(city_rank = ifelse(City %in% cities_ranked$City[1:10], "Top", "Other"))
data <- data |>
mutate(city_rank = ifelse(City %in% tail(cities_ranked, 10)$City, "Tail", city_rank))
data <- data |>
mutate(city_rank = factor(city_rank, levels = c("Top", "Tail")))
xlim <- c(
0,
max(data$Pre.Tax.TC)
)
data |>
inner_join(cities_ranked, by = c("City" = "City")) |>
filter(city_rank %in% c("Top", "Tail")) |>
ggplot(aes(
x = reorder(factor(City), Pre.Tax.TC, median),
y = Pre.Tax.TC
)) +
facet_wrap(~ as.factor(city_rank), scales = "free_y") +
geom_boxplot(aes(colour = median_salary)) +
scale_color_viridis_c(
trans = "log",
option = "plasma",
begin = 0.,
end = 0.85,
breaks = c(25000, 50000, 100000, 200000, 400000)
) +
theme_minimal() +
coord_cartesian(xlim = xlim) +
coord_flip() +
labs(
x = "",
y = ""
) +
theme(legend.position = "none") +
scale_y_continuous(labels = scales::comma)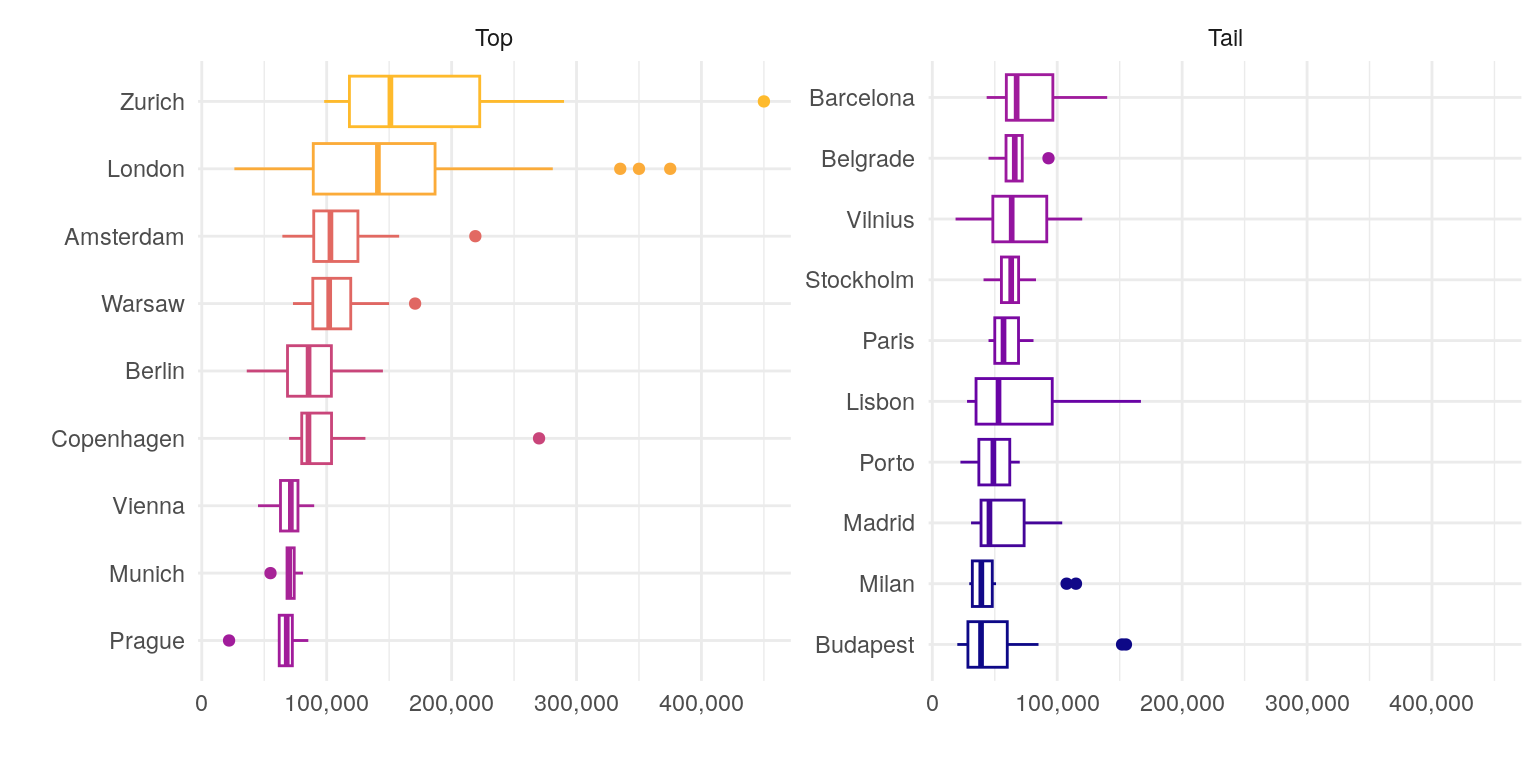
Salaries by Country and Job Title
Let’s visualize the median salary by country. Since salaries vary by position, it’s important to include job titles on the axis. However, with 249 distinct job titles, we need to group them into broader categories for clarity.
In the following plot, the size of the point represents the number of respondents, and the color represents the median salary. The text on the plot shows the median salary for each country and job category.
Show the code
data1 <- data |> inner_join(cities, by = c("City" = "name"))
data1 <- data1 |> left_join(read.csv("data/job-categories.csv"), by = "Job.Title")
country_job_title <- data1 |>
# Convert to long format
as_tibble() |>
group_by(Country, Job.Category) |>
summarize(
resp_count = n(),
median_salary = median(Pre.Tax.TC)
) |>
ungroup()
country_job_title |>
ggplot(aes(x = Job.Category, y = reorder(Country, desc(Country)))) +
geom_point(aes(size = resp_count, colour = median_salary), shape = 21, stroke = T, alpha = 0.9) +
scale_color_viridis_c(
trans = "log",
option = "plasma",
breaks = c(25000, 50000, 100000, 200000)
) +
scale_size_area(max_size = 8) +
geom_text(
aes(
y = as.numeric(as.factor(reorder(Country, desc(Country)))) - sqrt(resp_count) / 20,
label = format(median_salary, big.mark = ","),
),
vjust = 1.5,
hjust = 0.5,
colour = "grey30",
size = 2.5
) +
theme_minimal() +
theme(
axis.text.x = element_text(angle = 45, hjust = 1),
axis.ticks.y = element_blank(),
legend.position = "none",
# legend.position = "right",
# legend.key.height = unit(20, "pt"),
# legend.key.width = unit(5, "pt"),
# legend.box.margin = margin(0, 0, 0, 10),
# legend.title = element_blank()
) +
labs(x = NULL, y = NULL)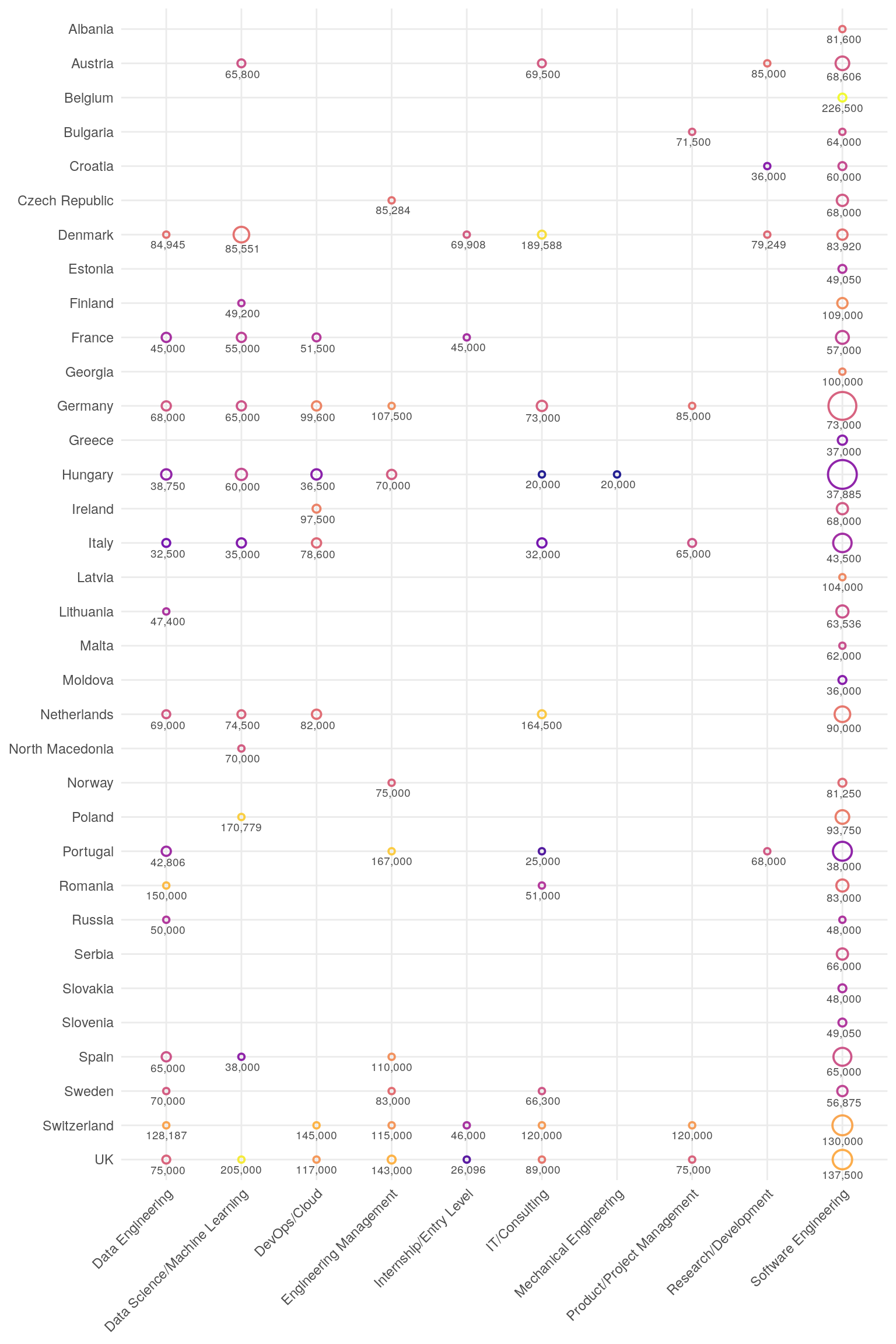
As we can see, salaries vary significantly by country and job title. Directly comparing salaries across these groups can be misleading due to differences in other influencing factors. To better understand the contribution of each factor, let’s build a linear regression model that accounts for these variables and potentially others, while controlling for confounding factors.
Show the code
data1 <- data |> inner_join(cities, by = c("City" = "name"))
data1 <- data1 |> left_join(read.csv("data/job-categories.csv"), by = "Job.Title")
model <- lm(Pre.Tax.TC ~ 0 + Country + Job.Category + Seniority, data = data1)Factors Affecting Salary
The linear model, built using Country, Job Category, and Seniority, demonstrates decent predictive power, with an adjusted R-squared value of 0.82. The model’s coefficients represent the effect (in USD) of each factor on salary. Let’s visualize these coefficients to gain a clearer understanding of the impact of each factor.
Show the code
library(tibble)
model_coef <- summary(model)$coefficients |>
data.frame() |>
rownames_to_column("value") |>
mutate(
effect = Estimate,
error = `Std..Error`,
p.value = `Pr...t..`,
significant = p.value < 0.05
)
model_coef <- model_coef |>
mutate(
variable = case_when(
str_detect(value, "Country") ~ "Country",
str_detect(value, "Job.Category") ~ "Job Category",
str_detect(value, "Seniority") ~ "Seniority"
)
)
model_coef <- model_coef |> mutate(value = sub("Country", "", value))
model_coef <- model_coef |> mutate(value = sub("Job.Category", "", value))
model_coef <- model_coef |> mutate(value = sub("Seniority", "", value))
country_coef <- model_coef |>
filter(variable == "Country") |>
arrange(desc(effect))
country_coef <- country_coef |> mutate(rownumber = 1:nrow(country_coef))
xlim <- c(
min(country_coef$effect - country_coef$error),
max(country_coef$effect + 1.1 * country_coef$error)
)
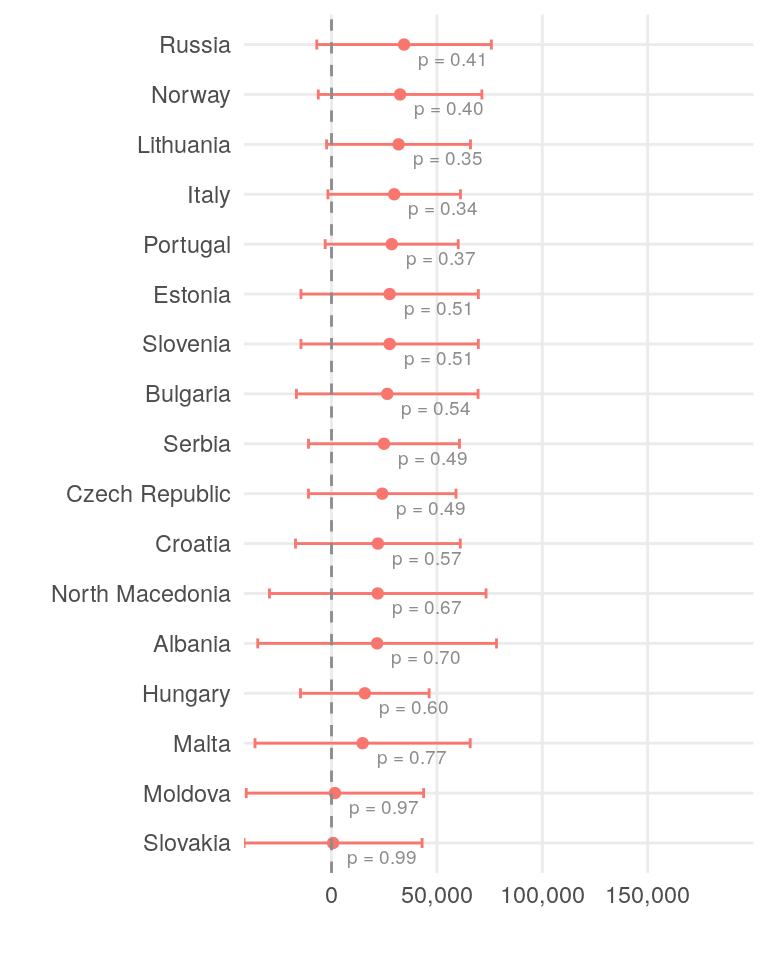
xscale <- c(0, 50000, 100000, 150000)The plot below illustrates the effect of each country on salary. The dot represents the estimated effect, while the error bars show the standard error. The color of the plot elements and the accompanying text indicate the significance of the effect. Only a few countries have a statistically significant impact on salary at the 0.05 level. However, it is generally better practice to consider the overall differences in salaries across countries.
Show the code
country_coef[1:17, ] |>
ggplot(aes(x = effect, y = reorder(value, effect), colour = significant)) +
geom_point() +
geom_errorbarh(aes(xmin = effect - error, xmax = effect + error),
height = .2
) +
geom_text(aes(label = paste("p =", format(p.value, digits = 2))),
vjust = 1.5,
hjust = -0.2,
colour = "grey55",
fill = "white",
size = 2.5
) +
geom_vline(
xintercept = 0,
linetype = "dashed",
colour = "grey55"
) +
theme_minimal() +
coord_cartesian(xlim = xlim) +
scale_x_discrete(limits = xscale, labels = scales::comma) +
theme(legend.position = "none") +
labs(x = "", y = "")
country_coef[18:34, ] |>
ggplot(aes(x = effect, y = reorder(value, effect), colour = significant)) +
geom_point() +
geom_errorbarh(aes(xmin = effect - error, xmax = effect + error),
height = .2
) +
geom_text(aes(label = paste("p =", format(p.value, digits = 2))),
vjust = 1.5,
hjust = -0.2,
colour = "grey55",
fill = "white",
size = 2.5
) +
geom_vline(
xintercept = 0,
linetype = "dashed",
colour = "grey55"
) +
theme_minimal() +
coord_cartesian(xlim = xlim) +
scale_x_discrete(limits = xscale, labels = scales::comma) +
theme(legend.position = "none") +
labs(x = "", y = "")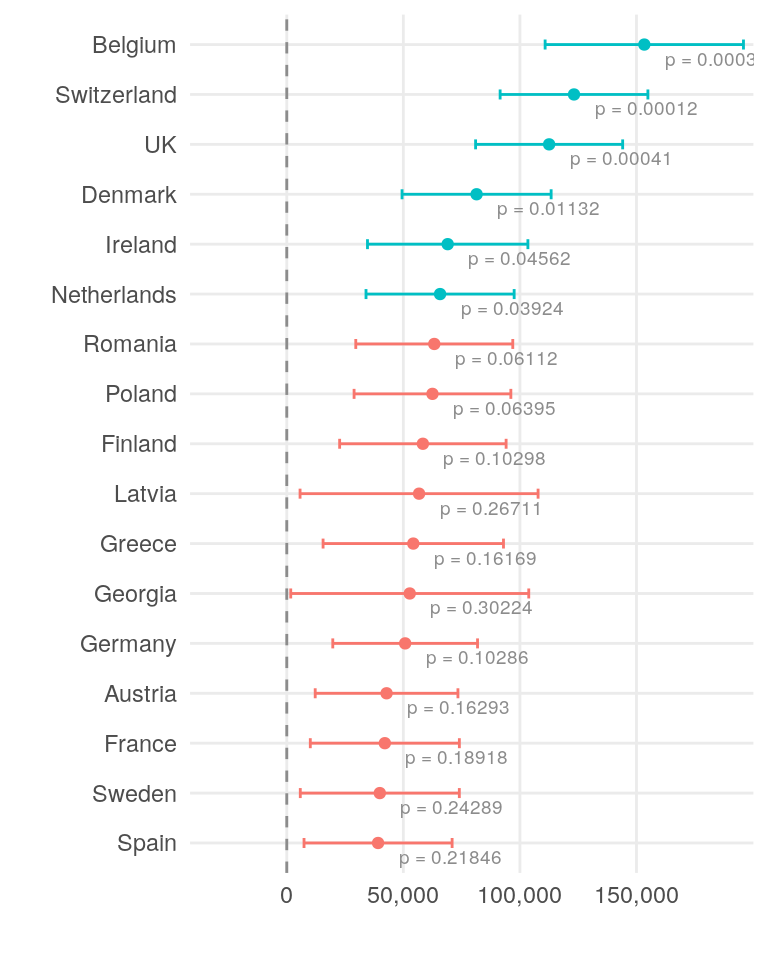
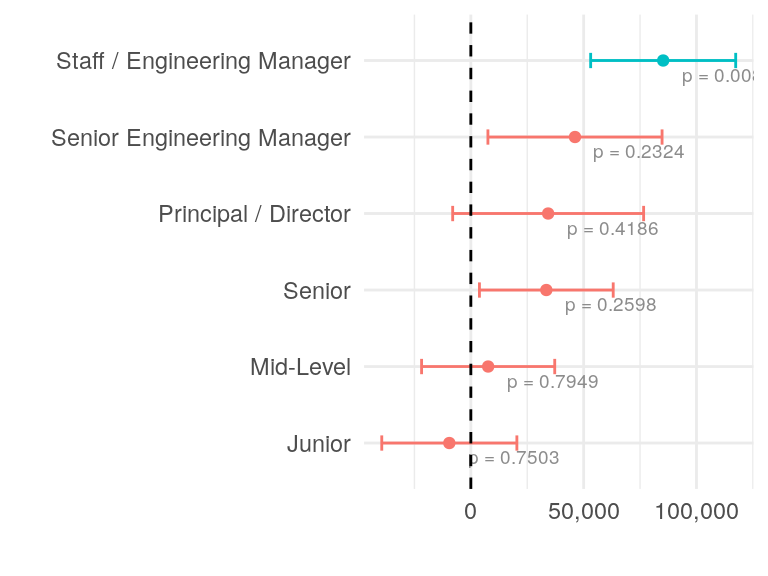
Next two plots show the effect of job category and seniority on the salary. The interpretation is similar to the previous plot.
Show the code
model_coef |>
filter(variable == "Job Category") |>
ggplot(aes(x = effect, y = reorder(value, effect), colour = significant)) +
geom_point() +
geom_errorbarh(aes(xmin = effect - error, xmax = effect + error),
height = .2
) +
geom_text(aes(label = paste("p =", format(p.value, digits = 2))),
vjust = 1.5,
hjust = -0.2,
colour = "grey55",
fill = "white",
size = 2.5
) +
geom_vline(xintercept = 0, linetype = "dashed") +
theme_minimal() +
scale_x_discrete(limits = c(-50000, 50000), labels = scales::comma) +
theme(legend.position = "none") +
labs(x = "", y = "")
model_coef |>
filter(variable == "Seniority") |>
mutate(value = str_replace(value, "Senior Staff / ", "")) |>
ggplot(aes(x = effect, y = reorder(value, effect), colour = significant)) +
geom_point() +
geom_errorbarh(aes(xmin = effect - error, xmax = effect + error),
height = .2
) +
geom_text(aes(label = paste("p =", format(p.value, digits = 2))),
vjust = 1.5,
hjust = -0.2,
colour = "grey55",
fill = "white",
size = 2.5
) +
geom_vline(
xintercept = 0,
linetype = "dashed"
) +
theme_minimal() +
theme(legend.position = "none") +
scale_x_discrete(limits = c(-50000, 50000)) +
labs(x = "", y = "") +
scale_x_continuous(labels = scales::comma)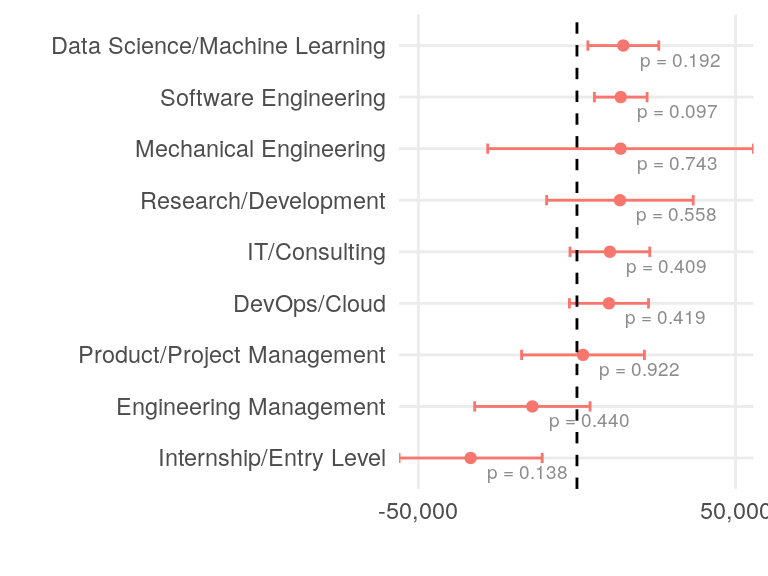
Taxation
Net salary is what matters most to employees, but it differs from gross salary. Taxes and social security contributions can significantly reduce take-home pay. Let’s calculate the net salary for each respondent and visualize the distribution of net salaries by country.
Show the code
library(tidyr)
net_by_country <- select(data, Country, City, Pre.Tax.TC, After.Tax.TC) |>
inner_join(cities, by = c("City" = "name")) |>
mutate(Tax = Pre.Tax.TC - After.Tax.TC) |>
group_by(Country) |>
summarise(
After.Tax.TC = mean(After.Tax.TC, na.rm = TRUE),
Tax = mean(Tax, na.rm = TRUE),
Net = After.Tax.TC,
Tax.Percent = Tax / (Net + Tax)
) |>
gather(key = "variable", value = "value", -Country, -Net, -Tax.Percent)
net_by_country$variable <-
factor(net_by_country$variable, levels = c("Tax", "After.Tax.TC"))
net_by_country$Country <-
factor(net_by_country$Country,
levels = unique(net_by_country$Country[order(net_by_country$Net)])
)
net_by_country |>
ggplot(aes(x = Country, y = value, fill = variable)) +
geom_col(width = 0.75, alpha = 0.9) +
geom_text(
aes(label = ifelse(variable == "Tax",
scales::percent(Tax.Percent, accuracy = 1), ""
)),
position = position_stack(vjust = 0.5),
colour = "grey30", size = 2.5
) +
coord_flip() +
theme_minimal() +
labs(x = "", y = "", fill = "") +
scale_y_continuous(labels = scales::comma)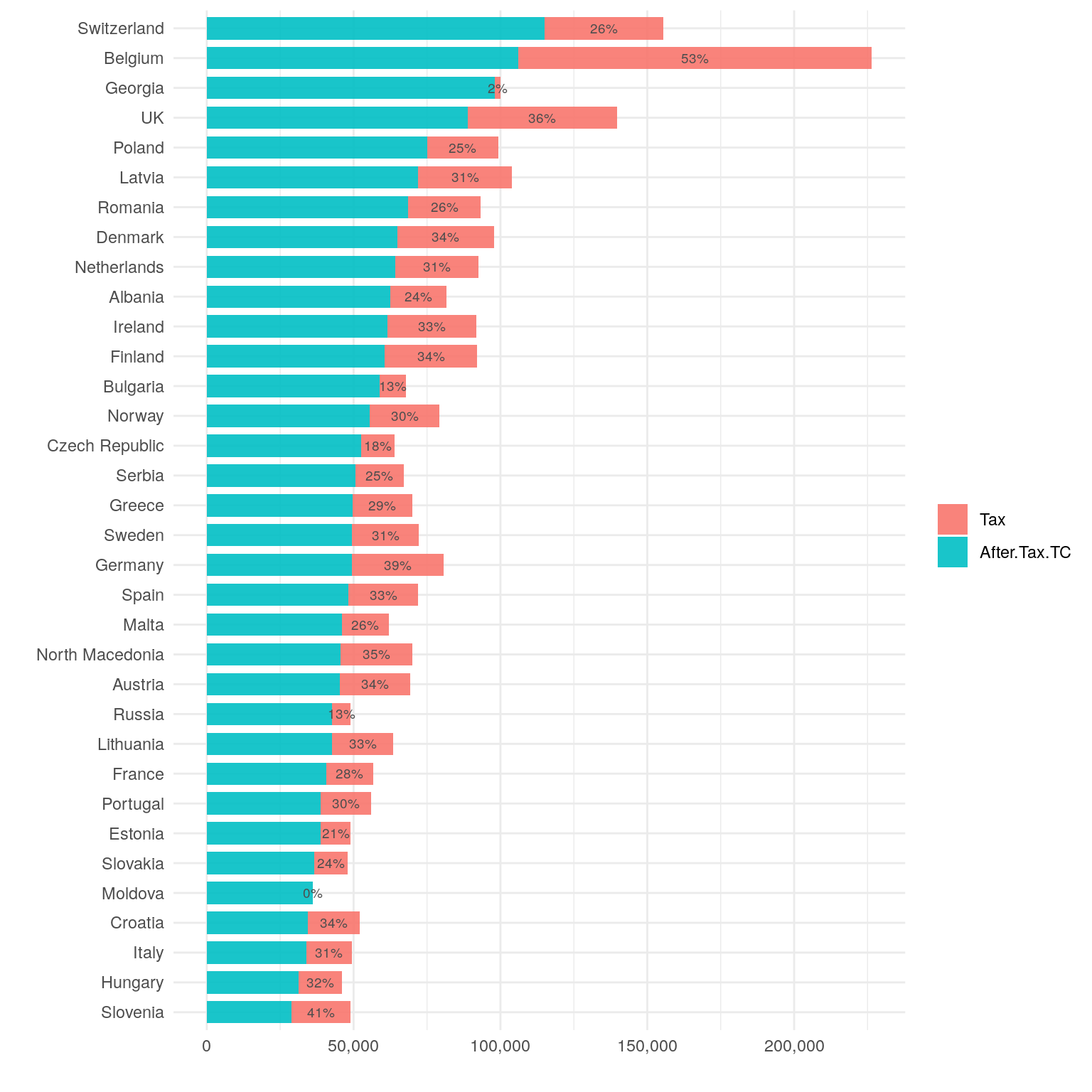
We can see that the tax burden varies significantly across countries. While the net salary is the most important factor for employees, it is also important to consider the cost of living in each country.
Cost of Living
We have net salary, but how far does it go in each country? Let’s calculate the cost of living for each respondent and visualize the distribution of costs by country.
We have the yearly savings for each respondent, which is the difference between the net salary and the cost of living. Having known household size and share of household expenses, we can calculate the cost of living for a household of a certain size. For this, we are going to employ the linear regression.
Show the code
data1 <- data |> inner_join(cities, by = c("City" = "name"))
# let's exclude unrealistic values
data1 <- data1 |> filter(Share.of.Household.Expenses > 10)
data1 <- data1 |> filter(Yearly.Savings < After.Tax.TC)
data1 <- data1 |> mutate(Cost.of.Living = (After.Tax.TC - Yearly.Savings) / Share.of.Household.Expenses * 100)
# let's convert Household.Size to a factor
data1 <- data1 |> mutate(Household.Size = as.factor(round(Household.Size)))
model <- lm(Cost.of.Living ~ 0 + Country + Household.Size, data = data1)
model_coef <- summary(model)$coefficients |>
data.frame() |>
rownames_to_column("value") |>
mutate(
effect = Estimate,
error = `Std..Error`,
p.value = `Pr...t..`,
significant = p.value < 0.05
)
model_coef <- model_coef |>
mutate(
variable = case_when(
str_detect(value, "Country") ~ "Country",
str_detect(value, "Household.Size") ~ "Household Size",
str_detect(value, "Lifestyle") ~ "Lifestyle"
)
)
model_coef <- model_coef |> mutate(value = sub("Country", "", value))
model_coef <- model_coef |> mutate(value = sub("Household.Size", "", value))
model_coef <- model_coef |> mutate(value = sub("Lifestyle", "", value))
country_coef <- model_coef |>
filter(variable == "Country") |>
arrange(desc(effect))
country_coef <- country_coef |>
mutate(rownumber = 1:nrow(country_coef))
xlim <- c(
min(country_coef$effect - country_coef$error),
max(country_coef$effect + 2 * country_coef$error)
)
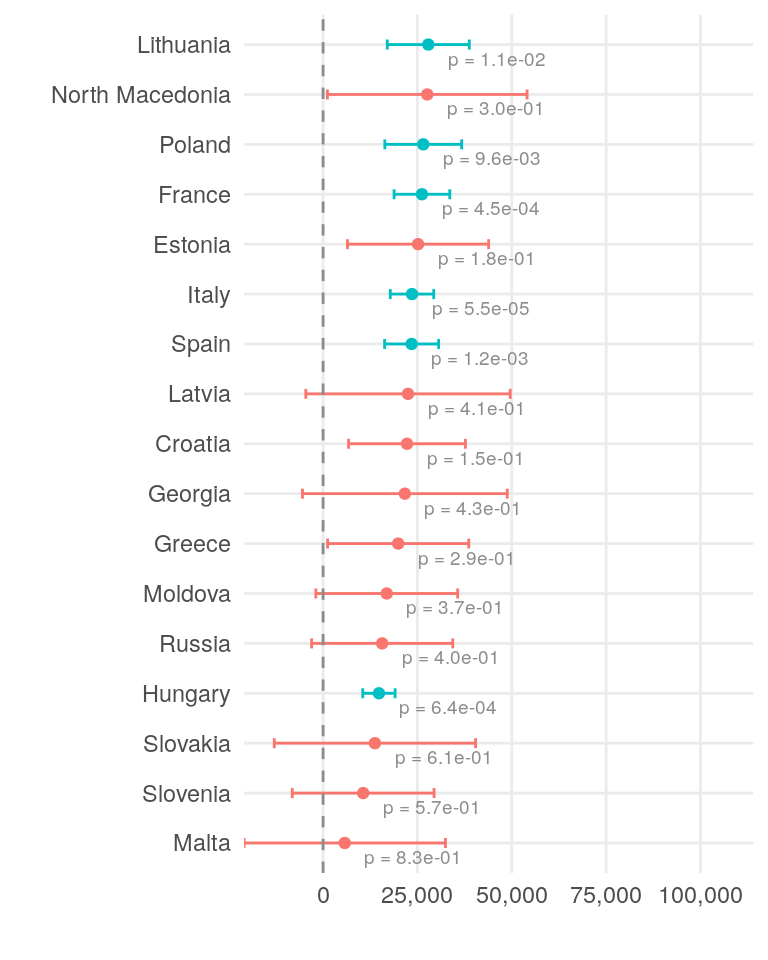
xscale <- c(0, 25000, 50000, 75000, 100000)The model Cost.of.Living ~ 0 + Country + Household.Size has an adjusted R-squared value of 0.75. We will not use Lifestyle as a factor in the model, as some of the levels have a small number of observations.
Let’s look at the coefficients for the country variable. Basically, the effect represents cost of living for a single person.
Show the code
country_coef[1:17, ] |>
ggplot(aes(x = effect, y = reorder(value, effect), colour = significant)) +
geom_point() +
geom_errorbarh(aes(xmin = effect - error, xmax = effect + error),
height = .2
) +
geom_text(aes(label = paste("p =", format(p.value, digits = 2))),
vjust = 1.5,
hjust = -0.2,
colour = "grey55",
fill = "white",
size = 2.5
) +
geom_vline(
xintercept = 0,
linetype = "dashed",
colour = "grey55"
) +
theme_minimal() +
coord_cartesian(xlim = xlim) +
scale_x_discrete(limits = xscale, labels = scales::comma) +
theme(legend.position = "none") +
labs(x = "", y = "")
country_coef[18:34, ] |>
ggplot(aes(x = effect, y = reorder(value, effect), colour = significant)) +
geom_point() +
geom_errorbarh(aes(xmin = effect - error, xmax = effect + error),
height = .2
) +
geom_text(aes(label = paste("p =", format(p.value, digits = 2))),
vjust = 1.5,
hjust = -0.2,
colour = "grey55",
fill = "white",
size = 2.5
) +
geom_vline(
xintercept = 0,
linetype = "dashed",
colour = "grey55"
) +
theme_minimal() +
coord_cartesian(xlim = xlim) +
scale_x_discrete(limits = xscale, labels = scales::comma) +
theme(legend.position = "none") +
labs(x = "", y = "")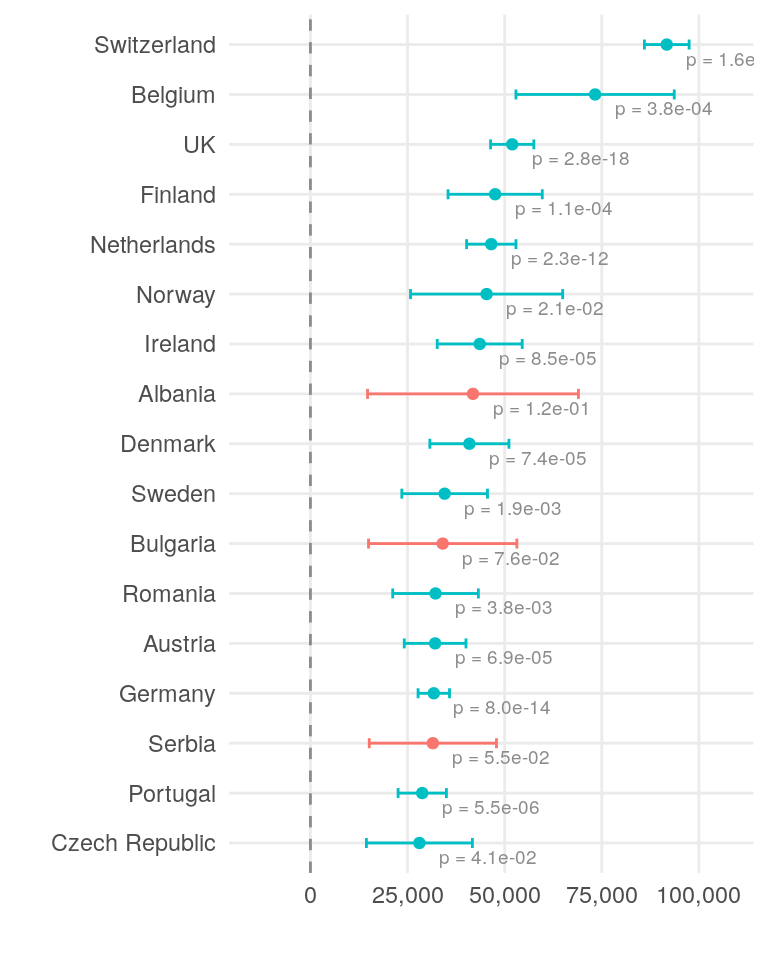
Next, we will look at the effect of household size on the cost of living. As expected, total cost of living for the two people is higher than for a single person, but the cost per person is lower for a larger household.
Show the code
xscale <- c(0, 10000, 20000, 30000, 40000, 50000)
xlim <- c(-10000, 60000)
model_coef |>
filter(variable == "Household Size") |>
ggplot(aes(x = effect, y = reorder(value, desc(value)), colour = significant)) +
geom_point() +
geom_errorbarh(aes(xmin = effect - error, xmax = effect + error),
height = .2
) +
geom_text(aes(label = paste("p =", format(p.value, digits = 2))),
vjust = 1.5,
hjust = -0.2,
colour = "grey55",
fill = "white",
size = 2.5
) +
geom_vline(
xintercept = 0,
linetype = "dashed",
colour = "grey55"
) +
theme_minimal() +
coord_cartesian(xlim = xlim) +
scale_x_discrete(limits = xscale, labels = scales::comma) +
theme(legend.position = "none") +
labs(x = "", y = "")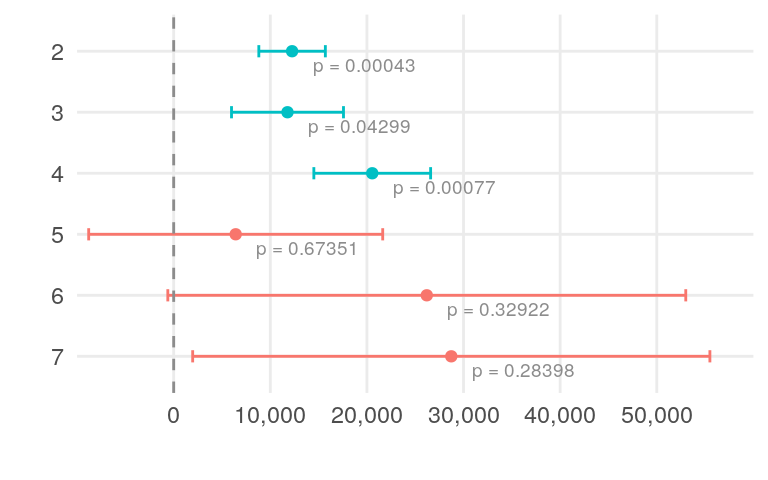
Savings
Finally, let’s look at the distribution of yearly savings by country. We will employ the same approach as before, using a linear regression model to understand the factors affecting savings. We will use Country, Household.Size, Job.Category, Seniority, and Share.of.Household.Expenses as predictors.
Show the code
data1 <- data |> inner_join(cities, by = c("City" = "name"))
# let's exclude unrealistic values
data1 <- data1 |> filter(Share.of.Household.Expenses > 10)
data1 <- data1 |> filter(Yearly.Savings < After.Tax.TC)
# let's convert Household.Size to a factor
data1 <- data1 |> mutate(Household.Size = as.factor(round(Household.Size)))
data1 <- data1 |> mutate(Share.of.Household.Expenses = Share.of.Household.Expenses / 100)
data1 <- data1 |> left_join(read.csv("data/job-categories.csv"), by = "Job.Title")
model <- lm(Yearly.Savings ~ 0 + Country + Household.Size + Job.Category + Seniority + Share.of.Household.Expenses, data = data1)
model_coef <- summary(model)$coefficients |>
data.frame() |>
rownames_to_column("value") |>
mutate(
effect = Estimate,
error = `Std..Error`,
p.value = `Pr...t..`,
significant = p.value < 0.05
)
model_coef <- model_coef |>
mutate(
variable = case_when(
str_detect(value, "Country") ~ "Country",
str_detect(value, "Household.Size") ~ "Household Size",
str_detect(value, "Lifestyle") ~ "Lifestyle"
)
)
model_coef <- model_coef |> mutate(value = sub("Country", "", value))
model_coef <- model_coef |> mutate(value = sub("Household.Size", "", value))
model_coef <- model_coef |> mutate(value = sub("Lifestyle", "", value))
country_coef <- model_coef |>
filter(variable == "Country") |>
arrange(desc(effect))
country_coef <- country_coef |> mutate(rownumber = 1:nrow(country_coef))
xlim <- c(
min(country_coef$effect - country_coef$error),
max(country_coef$effect + 1.2 * country_coef$error)
)
xscale <- c(0, 25000, 50000, 75000)This model performs on a mediocre level, with an adjusted R-squared value of 0.56. The coefficients for the country variable represent the expected yearly savings for a single person.
Show the code
country_coef[1:17, ] |>
ggplot(aes(x = effect, y = reorder(value, effect), colour = significant)) +
geom_point() +
geom_errorbarh(aes(xmin = effect - error, xmax = effect + error),
height = .2
) +
geom_text(aes(label = paste("p =", format(p.value, digits = 2))),
vjust = 1.5,
hjust = -0.2,
colour = "grey55",
fill = "white",
size = 2.5
) +
geom_vline(xintercept = 0, linetype = "dashed", colour = "grey55") +
theme_minimal() +
coord_cartesian(xlim = xlim) +
scale_x_discrete(limits = xscale, labels = scales::comma) +
theme(legend.position = "none") +
labs(x = "", y = "")
country_coef[18:34, ] |>
ggplot(aes(x = effect, y = reorder(value, effect), colour = significant)) +
geom_point() +
geom_errorbarh(aes(xmin = effect - error, xmax = effect + error),
height = .2
) +
geom_text(aes(label = paste("p =", format(p.value, digits = 2))),
vjust = 1.5,
hjust = -0.2,
colour = "grey55",
fill = "white",
size = 2.5
) +
geom_vline(
xintercept = 0,
linetype = "dashed",
colour = "grey55"
) +
theme_minimal() +
coord_cartesian(xlim = xlim) +
scale_x_discrete(limits = xscale, labels = scales::comma) +
theme(legend.position = "none") +
labs(x = "", y = "")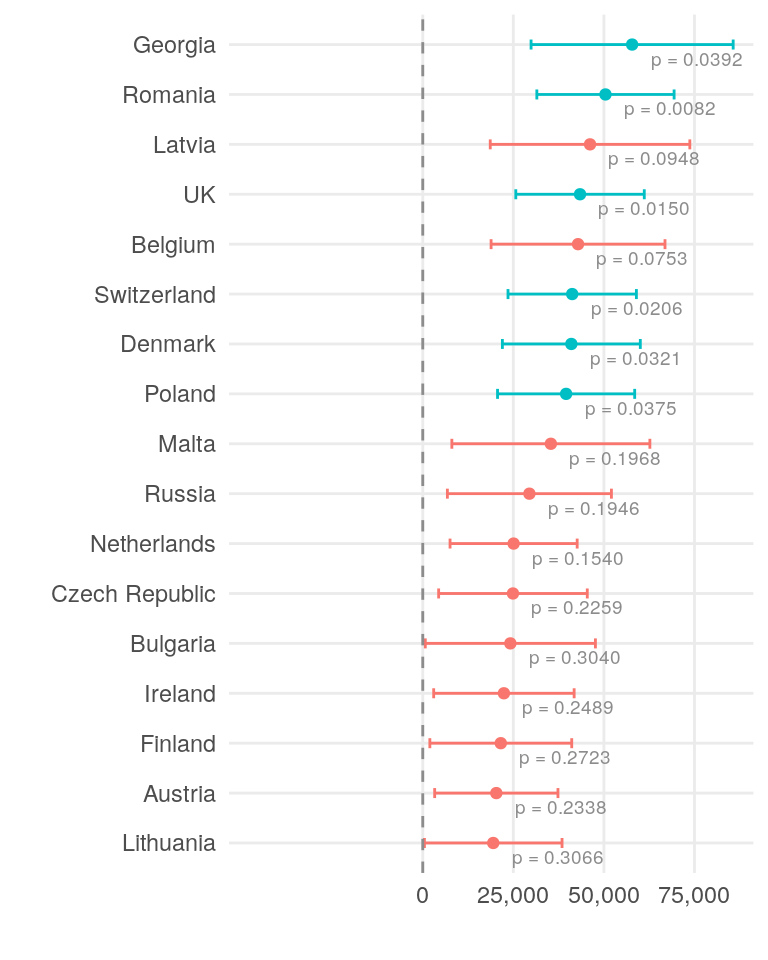
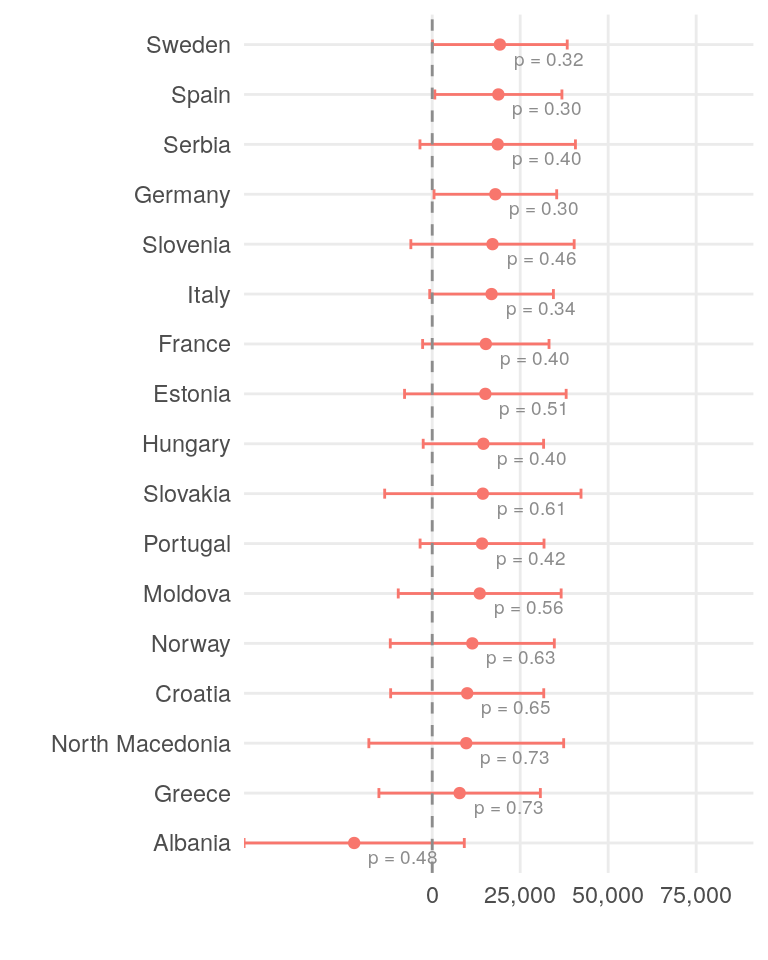
Only a few countries show a statistically significant impact on yearly savings. While differences in salary and cost of living across countries and roles are concrete factors, individual spending habits and lifestyle choices play an even more significant role in determining yearly savings.
Conclusion
This analysis offers several key insights. While the following conclusions are statistically significant at the 0.05 level, they may not apply to every individual case.
The top three countries for gross salary are Belgium, Switzerland, and the United Kingdom. These same countries also lead in net salary.
Belgium has the highest tax burden, followed by Germany and the UK.
Switzerland has the highest cost of living, with Belgium and the UK also ranking high. Hungary, Spain, and Italy are among the least expensive countries.
The highest yearly savings in the sample are found in Georgia and Romania, followed by the UK, Switzerland, and Denmark.