Introduction
In November 2024, the Yandex School of Data Analysis (YSDA) and Yandex conducted an open online intensive course on computer vision, focusing on generative diffusion models that underpin many visual services.
Format and Structure
Dates: November 25–29, 2024.
Format: All lectures and seminars were pre-recorded and broadcast on YouTube. During the broadcasts, participants could ask questions in the comments and interact with instructors and fellow participants via a dedicated Telegram channel.
Participation and Certification: The broadcasts were open to all without selection. However, to receive a certificate, participants needed to complete Qualifying assignments on the Yandex Contest platform and submit a final project.
Lectures and Seminars
The intensive course’s schedule consisted of lectures and seminars. Five days from Monday to Friday, in the evenings, there were a lecture for approximately an hour and then a seminar where the instructor provided with the implementation of the different aspects of image generation approaches.
November 25
Lecture 1: Introduction to Diffusion Models (Lecturer: Dmitry Baranchuk, Researcher, Yandex Research).
Seminar 1: Basic Implementation of Diffusion Models (Instructor: Sergey Kastrulin, Researcher, Yandex Research).
November 26
Lecture 2: Formulating Diffusion Models through Stochastic and Ordinary Differential Equations (Lecturer: Mikhail Romanov, Developer, Computer Vision Service).
Seminar 2: Implementing an Efficient Sampler (Instructor: Mikhail Romanov).
November 27
Lecture 3: Architectures of Diffusion Models, Training and Sampling Methods, and Text-to-Image Generation (Lecturer: Denis Kuznedelev, Researcher, Yandex Research).
Seminar 3: Generating Images from Text Descriptions (Instructor: Denis Kuznedelev).
November 28
Lecture 4: Distillation of Diffusion Models Using ODE-Based Methods (Lecturer: Nikita Starodubtsev, Researcher, Yandex Research ML Residency).
Lecture 5: Distillation of Diffusion Models Without ODEs (Lecturer: Dmitry Baranchuk).
Seminar 4: Implementing Consistent Models for Text-to-Image Generation (Instructor: Nikita Starodubtsev).
November 29
Lecture 6: Fine-Tuning Diffusion Models Using Reinforcement Learning Methods (Lecturer: Alexander Shishenya, Developer, Computer Vision Service).
Lecture 7: YandexART — Industrial Diffusion Model (Lecturer: Sergey Kastrulin).
Qualifying Assignment
The Qualifying Assignment was a prerequisite for accessing the final project and comprised three programming tasks designed to assess participants’ proficiency in fundamental machine learning concepts and PyTorch implementation.
1. Reshape a Tensor
The first task required reshaping a list or tensor by swapping its first two dimensions without utilizing PyTorch or NumPy methods. For example:
\(\begin{bmatrix}1 & 2 & 3\\4 & 5 & 6\end{bmatrix}\) should be transformed into \(\begin{bmatrix}1 & 4 \\ 2 & 5 \\ 3 & 6\end{bmatrix}\).
This task tested participants’ understanding of tensor manipulation at a fundamental level, emphasizing the importance of grasping underlying data structures without relying on high-level library functions.
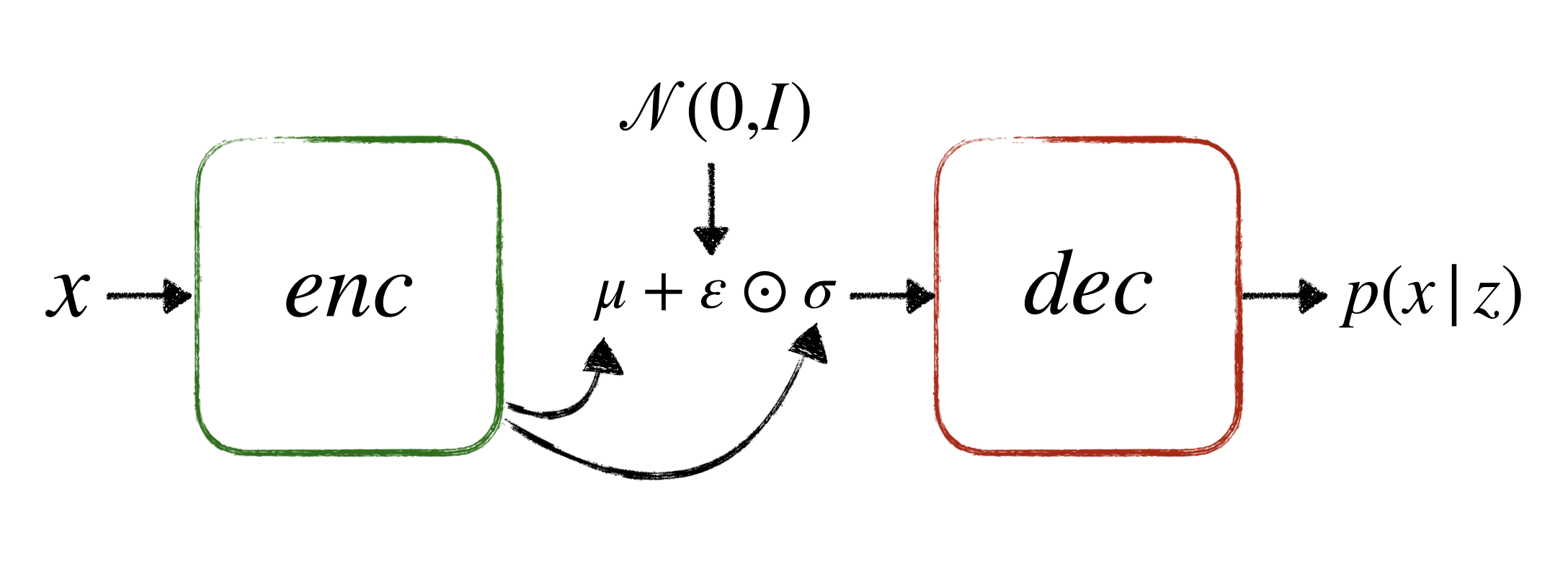
2. Encoder and Decoder Architecture
The second task involved implementing the encoder and decoder components of a Variational Autoencoder (VAE) architecture. VAEs are generative models that learn to represent data in a latent space, enabling the generation of new, similar data points. This task assessed participants’ ability to construct neural network architectures.
3. VAE Loss Function
The third task required identifying and correcting errors in the VAE loss function implementation. To validate the correctness of the function, participants trained the VAE and performed inference on the MNIST digits dataset. The VAE loss function typically comprises two components:
Reconstruction Loss: Measures how well the decoder reconstructs the input data.
Kullback-Leibler (KL) Divergence: Regularizes the learned latent space to align with a predefined distribution, often a standard normal distribution.
Accurate implementation of this loss function is crucial for the VAE to learn meaningful latent representations and generate coherent outputs.

Each of the first two tasks was worth up to 2 points, while the third task could earn up to 4 points. A minimum of 6 points was required to pass, ensuring that participants had a solid grasp of the necessary concepts to proceed to the final project.
Final Project
In the final project, participants had to distill a multi-step diffusion model into a more efficient, few-step student model, significantly enhancing generation speed.
The project focused on implementing the Consistency Distillation framework, a method that accelerates diffusion models by enforcing self-consistency along learned trajectories.
Participants would apply this technique to distill the Stable Diffusion 1.5 (SD 1.5) model, a latent text-to-image diffusion model capable of generating photo-realistic images from textual descriptions.
The project comprised eight tasks, each building upon the previous, guiding participants toward developing a proficient model capable of generating images in just four steps.
Teacher Model
The initial model for our experiments is Stable Diffusion 1.5, a pre-trained latent text-to-image diffusion model. This serves as the “teacher” model in our distillation process.
For the prompt: “A sad puppy with large eyes”, running the model with 50 steps and a guidance_scale of 7.5 produces the following high-quality images:

However, when the number of steps is reduced to 4, the output becomes blurry and lacks detail:

This demonstrates the trade-off between the number of sampling steps and image quality in diffusion models. Our goal is to bridge this gap by using techniques like Consistency Distillation to achieve similar quality with fewer steps.
Consistency Training
The model will be trained on a subset of the COCO Dataset comprising 5,000 images. To reduce memory consumption, we will train LoRA (Low-Rank Adaptation) adapters for the U-Net convolutional neural network instead of fine-tuning the entire model.
This approach significantly decreases the number of trainable parameters and activation memory, enhancing efficiency during training.
Additionally, implementing techniques such as gradient checkpointing can further reduce memory usage, albeit with a potential increase in training time.
By employing these strategies, we aim to achieve effective model performance while operating within the memory constraints of our training environment.
The result with guidance_scale = 2 looks sharper, but the quality is still far from desired.

Consistency Distillation
In the Consistency Distillation phase, we enhance the model’s quality by incorporating a teacher model within the U-Net architecture, utilizing LoRA adapters trained in the previous step. This integration refines the student’s learning process, leading to significantly improved image generation results.
Consistency Distillation is a technique that accelerates diffusion models by enforcing self-consistency along learned trajectories. By aligning the student model’s outputs with those of the teacher model, the student learns to produce high-quality images in fewer steps. Implementing this method with LoRA adapters allows for efficient training, as LoRA reduces the number of trainable parameters, thereby decreasing memory consumption and computational load.

Multi-boundary Consistency Distillation
In the Multi-boundary Consistency Distillation phase, we draw inspiration from recent advancements in generative modeling, particularly the work by researchers from Google DeepMind. In their paper “Multistep Consistency Models” (arXiv:2403.06807v3), they propose a method that interpolates between consistency models and diffusion models, allowing for a trade-off between sampling speed and quality.
By employing 2 to 8 sampling steps, this approach achieves performance comparable to traditional diffusion models but with significantly reduced computational resources. This reduction in sampling steps leads to decreased memory usage and computational load, making the models more efficient without compromising output quality.
Implementing this technique involves training the model to maintain consistency across multiple steps, effectively enabling it to generate high-quality samples in fewer iterations. This advancement is particularly beneficial for applications requiring rapid generation or operating under resource constraints.

Graded Assignments
There were 4 automatically graded assignments and one teacher graded assignment.
1. Implementation of DDIM Solver Step
In diffusion models, the forward diffusion process gradually transforms images into noise, following the distribution:
\[ q(\mathbf{x}_t | \mathbf{x}_0)= {N}(\mathbf{x}_t | \alpha_t \mathbf{x}_0, \sigma^2_t I)\]
At time step \(t\), the noisy image \(\mathbf{x}_t\) can be represented as: \(\mathbf{x}_t = \alpha_t \mathbf{x}_0 + \sigma_t \epsilon\), where \(\epsilon{\sim} {N}(0, I)\).
The goal of the diffusion model is to solve the inverse problem, reconstructing an image from noise. This reverse process is formulated as an ordinary differential equation (ODE):
\(dx = \left[ f(\mathbf{x}, t) - \frac{1}{2} \nabla_{\mathbf{x}_t} \log p_t(\mathbf{x}) \right] dt\), where \(f(\mathbf{x}, t)\) is known from the given noise process, and \(\nabla_{\mathbf{x}_t} \log p_t(\mathbf{x}_t)\) (score function) is estimated using a neural network: \(s_\theta(\mathbf{x}_t, t) \approx \nabla_{\mathbf{x}_t} \log p_t(\mathbf{x}_t)\).
Thus, having an estimate for \(\nabla_{\mathbf{x}_t} \log p_t(\mathbf{x})\), we can solve this ODE starting from random noise and generate a picture.
For this assignment, participants implemented the step from \(\mathbf{x}_t\) to \(\mathbf{x}_s\) using the Denoising Diffusion Implicit Models (DDIM) framework:
\[\mathbf{x}_s = DDIM(\epsilon_\theta, \mathbf{x}_t, t, s) = \alpha_s \cdot \left(\frac{\mathbf{x}_t - \sigma_t \epsilon_\theta}{\alpha_t} \right) + \sigma_s \epsilon_\theta\]
Most of the function was pre-written by the instructors, but participants were required to correctly set \(\alpha_t\) and \(\sigma_t\) using the DDIMScheduler. This task tested participants’ understanding of the underlying mathematical concepts and their ability to implement them in code.
2. Implementation of Noise Process
The second task involved implementing the function q_sample(x, t, scheduler, noise) to simulate the forward diffusion process. The function follows the mathematical formulation:
\(q(\mathbf{x}_t | \mathbf{x}_0)= {N}(\mathbf{x}_t | \alpha_t \mathbf{x}_0, \sigma^2_t I)\) where the noisy image \(x_t\) at time \(t\) is calculated as:
\(\mathbf{x}_t = \alpha_t \mathbf{x}_0 + \sigma_t \epsilon\), where \(\epsilon{\sim} {N}(0, I)\).
Participants were required to:
Use the scheduler to retrieve \(\alpha_t\) and \(\sigma_t\) values for the given timestep \(t\).
Generate random noise \(\epsilon \sim \mathcal{N}(0, I)\) and apply it to the formula above to simulate the noisy image \(\mathbf{x}_t\).
Handle edge cases for boundary points, ensuring the process remains valid when \(t=0\).
This assignment focused on implementing the forward diffusion process accurately while accounting for the nuances of boundary conditions, which added complexity to the task.
3. Consistency Training
Consistency distillation leverages the teacher model to obtain the second point on the ODE trajectory, which can also be computed using the DDIM formula. The task required participants to derive the function for this computation based on the definitions of the noise process and the score function.
\(\epsilon_\theta(x_t, t) = - \sigma_t s_\theta(x_t, t)\)
\(s_\theta(x_t, t) \approx \nabla_{x_t} \log q(x_t) = \mathop{\mathbb{E}}_{\mathbf{x}\sim p_{data}}\left [ \nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t | \mathbf{x}) \vert \mathbf{x}_t \right ] \approx \nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t \vert \mathbf{x})\)
4. Multi-boundary Timesteps
The objective of this task was to implement the get_multi_boundary_timesteps function, which generates boundary points for multi-step consistency training. These boundary points define the timesteps used in sampling and play a critical role in the effectiveness of the distillation process.
The task itself was somewhat ambiguous, leaving room for interpretation. Participants were expected to:
- Understand how multi-boundary timesteps are utilized in multi-step consistency models. Implement the function to output the appropriate boundary points.
- Ensure that the timesteps are well-distributed and align with the requirements of the consistency distillation framework.
5. Generated Images
Once all the graded and non-graded tasks were completed, the next step was to train the Multi-boundary Consistency Model. This involved applying the techniques and frameworks developed in earlier tasks to produce high-quality generated images.
After training, participants were required to upload the trained model along with generated results for assessment. This provided an opportunity to showcase the practical implementation of multi-step consistency techniques.
The trained model was evaluated based on its ability to generate images that were consistent and high-quality, even with a reduced number of sampling steps.
Sampling Prompts
- A sad puppy with large eyes.
- Astronaut in a jungle, cold color palette, muted colors, detailed, 8k.
- A photo of beautiful mountain with realistic sunset and blue lake, highly detailed, masterpiece.
- A girl with pale blue hair and a cami tank top.
- A lighthouse in a giant wave, origami style.
- Belle epoque, christmas, red house in the forest, photo realistic, 8k.
- A small cactus with a happy face in the Sahara desert.
- Green commercial building with refrigerator and refrigeration units outside.
Conclusion
Participating in YSDA’s intensive training programs has been both challenging and rewarding. My first experience was during GPT Week in 2023, which did not require a qualifying assignment. The final project involved training a model to summarize articles, with flexibility regarding the architecture and implementation details.
In contrast, CV Week 2024 presented a more rigorous experience. Both the qualifying assignment and the final project demanded significant effort, especially given my limited background in computer vision. This intensive pushed me to expand my knowledge and skills, making the experience both demanding and educational.
For those interested in exploring similar topics, YSDA offers a range of online courses. These resources can provide a solid foundation for tackling advanced subjects in data analysis and machine learning.
Source code and presentations can be found in my GitHub repository: CV_Week.

