Propensity Score Matching for Causal Analysis

A hands-on guide to implementing propensity score matching in R for causal inference in A/B testing scenarios using marketing data.
A/B Testing
Statistics
R
Author

Aleksei Prishchepo

Published

October 31, 2025

In marketing analytics, one of the most common questions is:

Did our campaign actually cause people to subscribe, or the subscribers were already more likely to do so?

When we only have observational data — not a randomized experiment — it’s tricky to separate correlation from causation. This is where Propensity Score Matching (PSM) comes in.

In this tutorial, we’ll use the Bank Marketing dataset from the UCI Machine Learning Repository to estimate the causal effect of being previously contacted on the probability of subscribing to a term deposit.

We’ll use the R package MatchIt to perform matching and evaluate balance.

Data Overview

First, let’s load the necessary libraries and the dataset.

Load Packages

library(MatchIt)
library(tidyverse)
library(lubridate)
library(ggplot2)
library(readr)
library(skimr)
library(here)

Load Data

Here we download the UCI Bank Marketing dataset if it’s not already present in the working directory.

if (file.exists(here("bank-full.csv"))) {
  dataset <- read.csv(file.path(here(), "bank-full.csv"), sep = ";")
} else {
  url <- "https://archive.ics.uci.edu/static/public/222/bank+marketing.zip"
  temp <- tempfile()
  download.file(url, temp)
  unzip(temp, "bank.zip", exdir = here())
  unzip(here("bank.zip"), "bank-full.csv", exdir = here())
  dataset <- read.csv(file.path(here(), "bank-full.csv"), sep = ";")
  unlink(temp)
}
dataset |> glimpse()
Rows: 45,211
Columns: 17
$ age       <int> 58, 44, 33, 47, 33, 35, 28, 42, 58, 43, 41, 29, 53, 58, 57, …
$ job       <chr> "management", "technician", "entrepreneur", "blue-collar", "…
$ marital   <chr> "married", "single", "married", "married", "single", "marrie…
$ education <chr> "tertiary", "secondary", "secondary", "unknown", "unknown", …
$ default   <chr> "no", "no", "no", "no", "no", "no", "no", "yes", "no", "no",…
$ balance   <int> 2143, 29, 2, 1506, 1, 231, 447, 2, 121, 593, 270, 390, 6, 71…
$ housing   <chr> "yes", "yes", "yes", "yes", "no", "yes", "yes", "yes", "yes"…
$ loan      <chr> "no", "no", "yes", "no", "no", "no", "yes", "no", "no", "no"…
$ contact   <chr> "unknown", "unknown", "unknown", "unknown", "unknown", "unkn…
$ day       <int> 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, …
$ month     <chr> "may", "may", "may", "may", "may", "may", "may", "may", "may…
$ duration  <int> 261, 151, 76, 92, 198, 139, 217, 380, 50, 55, 222, 137, 517,…
$ campaign  <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
$ pdays     <int> -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, …
$ previous  <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ poutcome  <chr> "unknown", "unknown", "unknown", "unknown", "unknown", "unkn…
$ y         <chr> "no", "no", "no", "no", "no", "no", "no", "no", "no", "no", …

Data Summary

dataset |> skim()
Data summary
Name dataset
Number of rows 45211
Number of columns 17
_______________________
Column type frequency:
character 10
numeric 7
________________________
Group variables None

Variable type: character

skim_variable n_missing complete_rate min max empty n_unique whitespace
job 0 1 6 13 0 12 0
marital 0 1 6 8 0 3 0
education 0 1 7 9 0 4 0
default 0 1 2 3 0 2 0
housing 0 1 2 3 0 2 0
loan 0 1 2 3 0 2 0
contact 0 1 7 9 0 3 0
month 0 1 3 3 0 12 0
poutcome 0 1 5 7 0 4 0
y 0 1 2 3 0 2 0

Variable type: numeric

skim_variable n_missing complete_rate mean sd p0 p25 p50 p75 p100 hist
age 0 1 40.94 10.62 18 33 39 48 95 ▅▇▃▁▁
balance 0 1 1362.27 3044.77 -8019 72 448 1428 102127 ▇▁▁▁▁
day 0 1 15.81 8.32 1 8 16 21 31 ▇▆▇▆▆
duration 0 1 258.16 257.53 0 103 180 319 4918 ▇▁▁▁▁
campaign 0 1 2.76 3.10 1 1 2 3 63 ▇▁▁▁▁
pdays 0 1 40.20 100.13 -1 -1 -1 -1 871 ▇▁▁▁▁
previous 0 1 0.58 2.30 0 0 0 0 275 ▇▁▁▁▁

Correlation Matrix

library(PerformanceAnalytics)

set.seed(123)

dataset |>
  sample_n(1000) |>
  select_if(is.numeric) |>
  chart.Correlation(histogram = TRUE, pch = "+")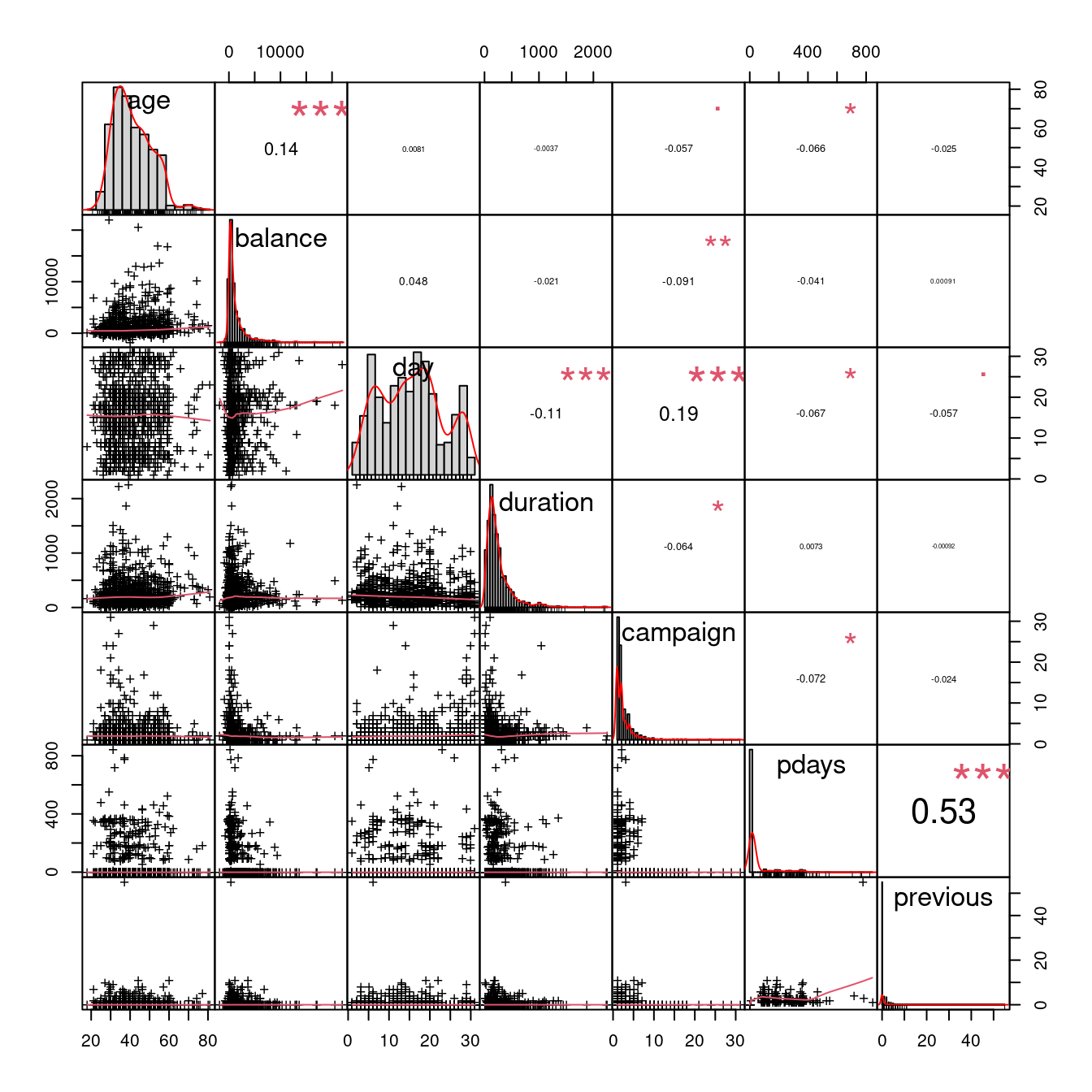
Figure 1: Distributions and correlations of numeric variables in the dataset.

Defining Treatment and Outcome

Our treatment variable will be whether the client was previously contacted (pdays != -1), and the outcome variable will be whether the client subscribed to a term deposit (y == "yes").

dataset <- dataset |>
  mutate(
    treat = ifelse(pdays != -1, 1, 0),    # previously contacted
    outcome = ifelse(y == "yes", 1, 0)
  )

  • treat = 1: client was previously contacted (pdays != -1);

  • treat = 0: new client, not contacted before;

  • outcome = 1: client subscribed to term deposit;

  • outcome = 0: client did not subscribe.

Let’s check the basic rates:

dataset |>
  group_by(treat) |>
  summarise(
    n = n(),
    subscription_rate = mean(outcome)
  )
# A tibble: 2 × 3
  treat     n subscription_rate
  <dbl> <int>             <dbl>
1     0 36954            0.0916
2     1  8257            0.231

We can clearly see that previously contacted clients (treat = 1) have a higher subscription rate — but this might be due to other factors like income or engagement.

t_test_all <- t.test(outcome ~ treat, data = dataset)
t_test_all

    Welch Two Sample t-test

data:  outcome by treat
t = -28.552, df = 10051, p-value < 2.2e-16
alternative hypothesis: true difference in means between group 0 and group 1 is not equal to 0
95 percent confidence interval:
 -0.1486926 -0.1295874
sample estimates:
mean in group 0 mean in group 1 
     0.09157331      0.23071333

Covariates and Model Formula

We include demographic and financial variables that can influence both being re-contacted and subscribing. We need to exclude campaign (number of contacts performed during this campaign and for this client), contact (contact communication type), previous (number of contacts performed before this campaign), and poutcome (outcome of the previous marketing campaign) to avoid leaking information about treatment assignment.

formula <- treat ~ age + job + marital + education + default +
  balance + housing + loan

Estimating Propensity Scores and Matching

We now fit the PSM model using nearest-neighbor matching:

psm <- matchit(
  formula,
  data = dataset,
  method = "nearest",
  ratio = 1
)

Let’s inspect the summary. We won’t include the whole output of the summary function, just the number of matched pairs:

summary(psm)$nn
              Control Treated
All (ESS)       36954    8257
All             36954    8257
Matched (ESS)    8257    8257
Matched          8257    8257
Unmatched       28697       0
Discarded           0       0

Visualizing Balance

plot(psm, type = "jitter", interactive = FALSE)
Figure 2: Plot of propensity scores before and after matching. 
plot(psm, type = "density", interactive = FALSE,
     which.xs = ~ age + job + marital + education + default + balance + 
    housing + loan)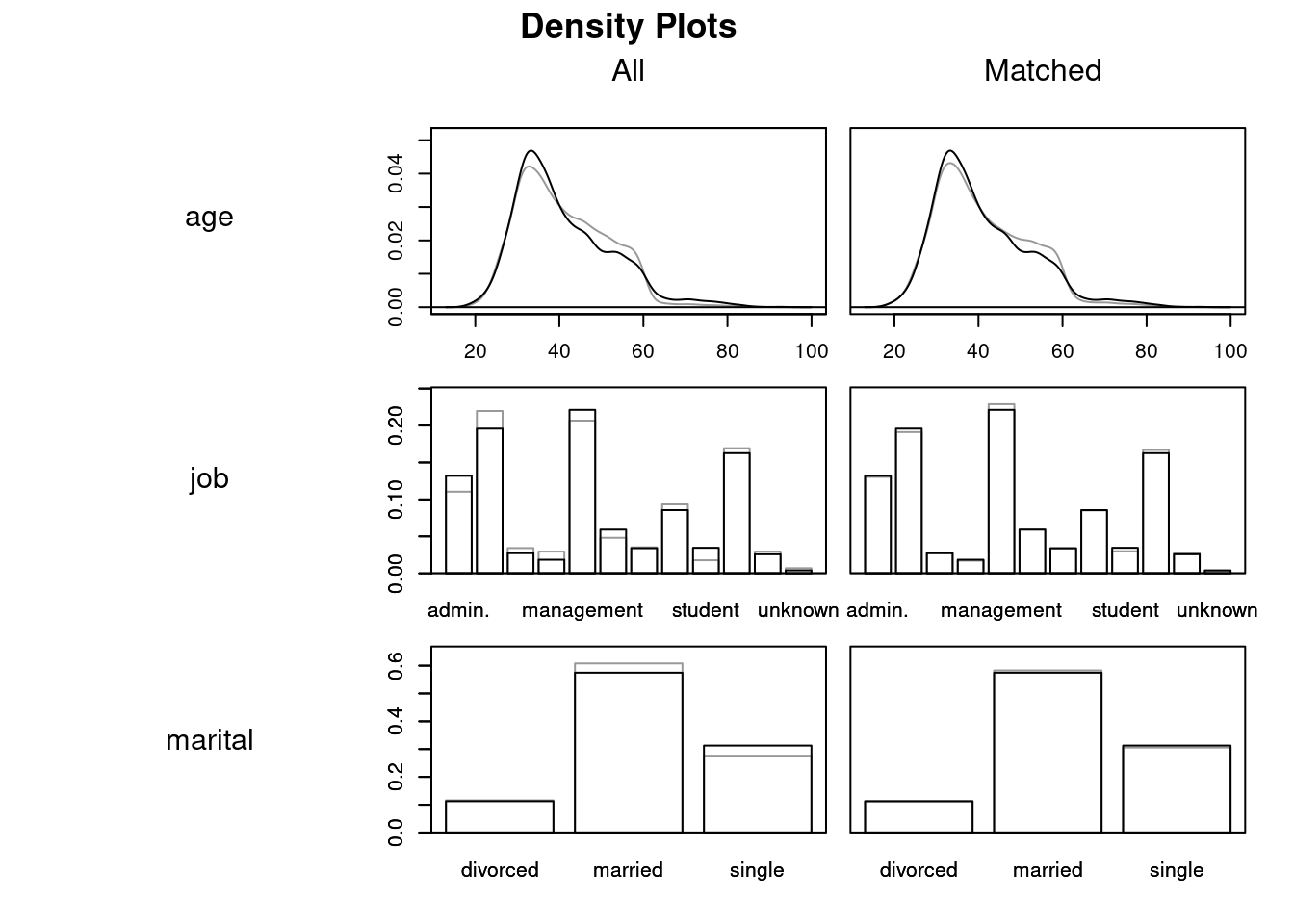
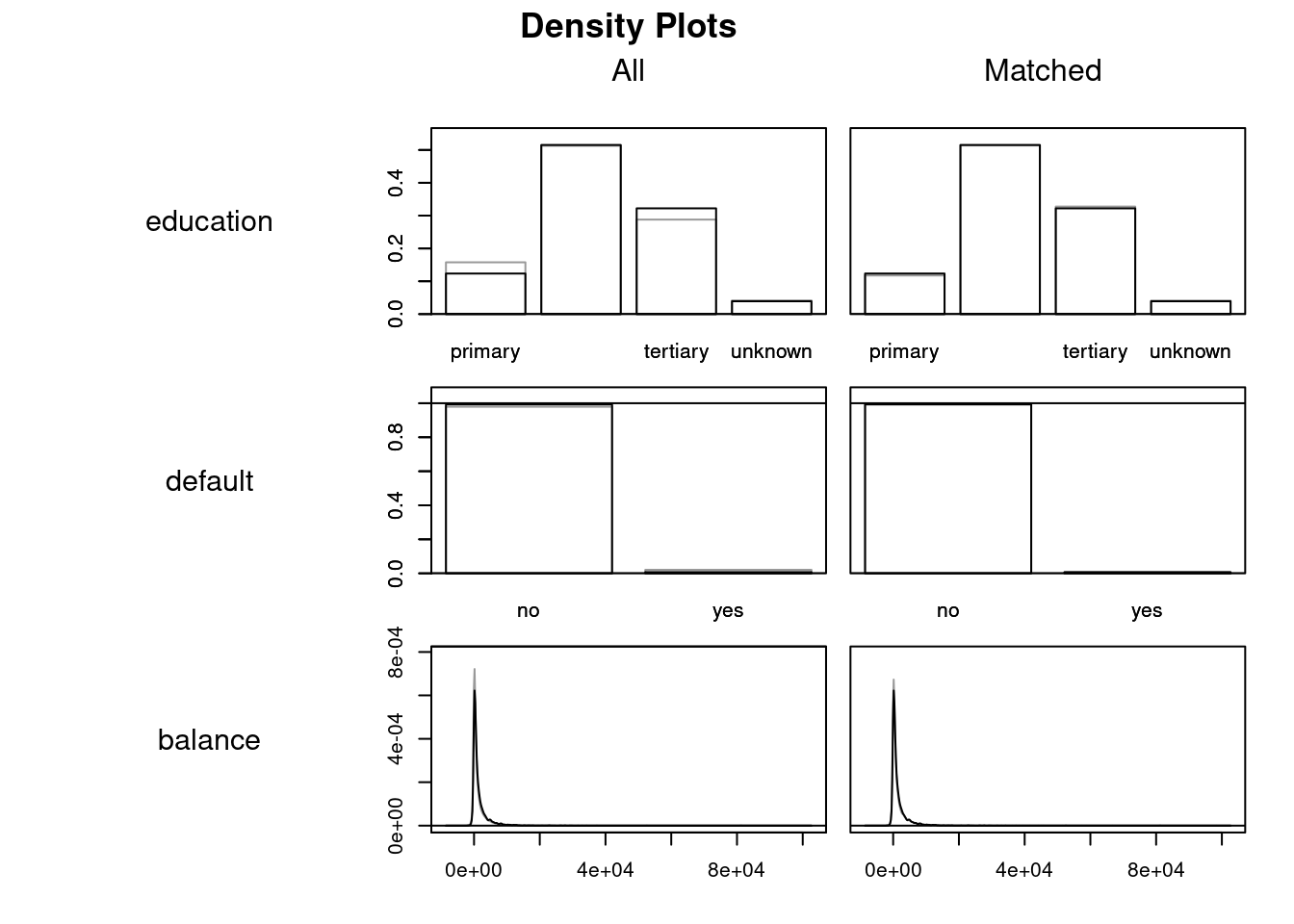
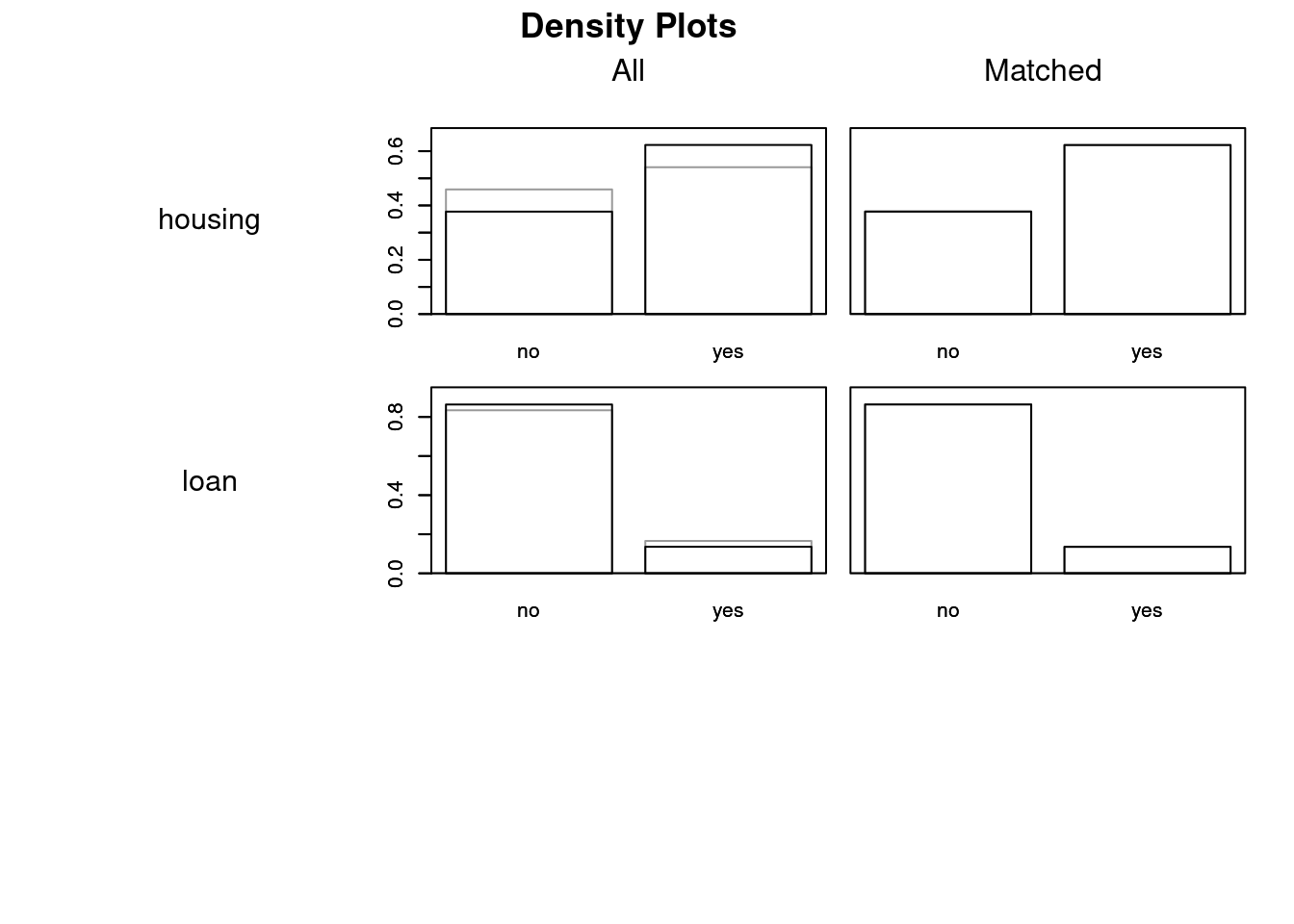
Figure 3: Density plots of variables before and after matching.
Figure 4: Density plots of variables before and after matching.
Figure 5: Density plots of variables before and after matching. 
library(cobalt)

love.plot(psm, threshold = 0.1)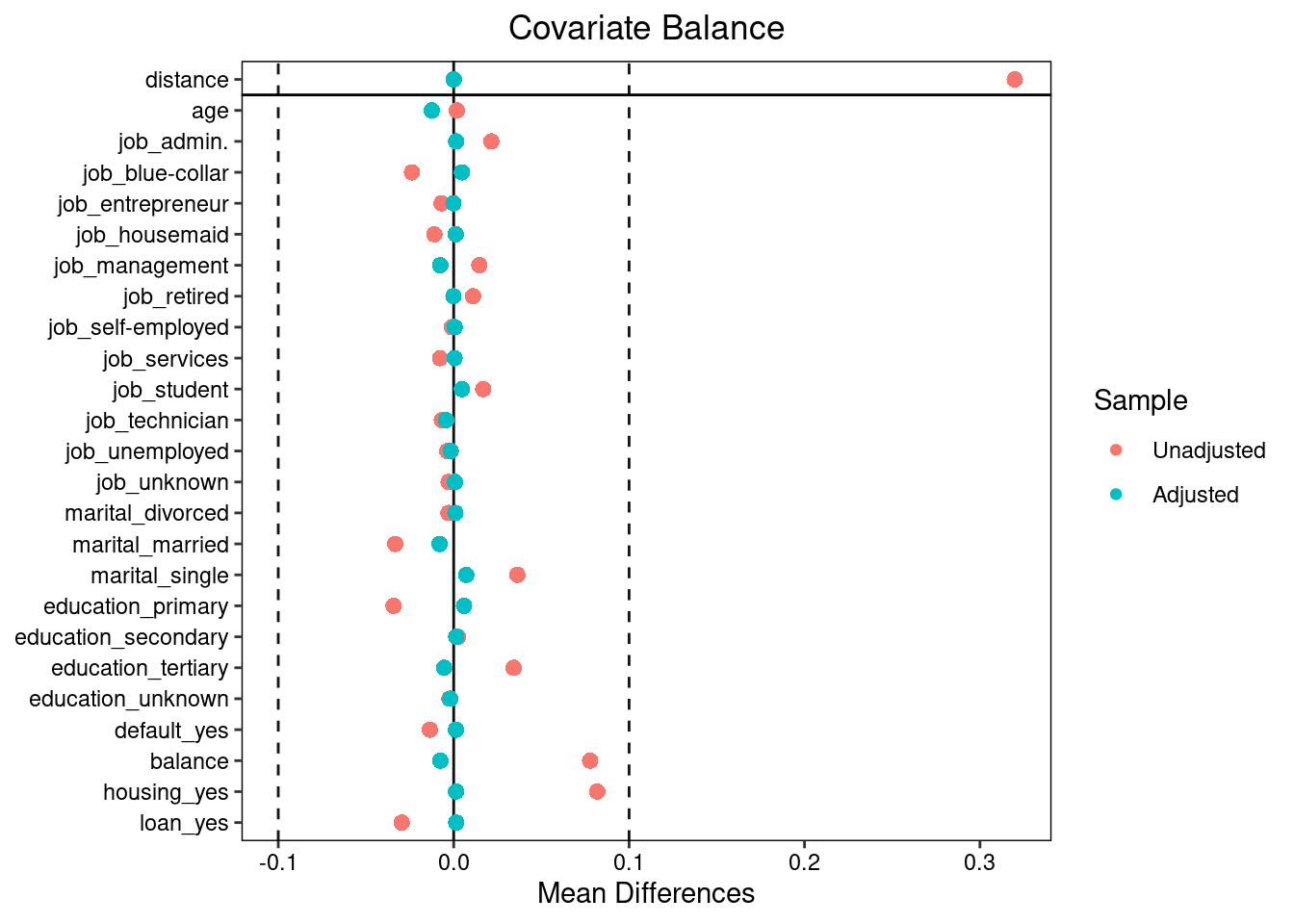
Figure 6: Love plot showing standardized mean differences before and after matching.

Estimating the Treatment Effect

Extract the matched data and estimate the effect on subscription:

matched_data <- match.data(psm)  
t_test <- t.test(outcome ~ treat, data = matched_data)
t_test

    Welch Two Sample t-test

data:  outcome by treat
t = -18.501, df = 15563, p-value < 2.2e-16
alternative hypothesis: true difference in means between group 0 and group 1 is not equal to 0
95 percent confidence interval:
 -0.1201447 -0.0971255
sample estimates:
mean in group 0 mean in group 1 
      0.1220782       0.2307133

The difference in means represents the Average Treatment Effect on the Treated (ATT) — how much more likely previously contacted customers are to subscribe, compared to similar new customers.

diff_means <- unname(t_test$estimate[2] - t_test$estimate[1])
diff_means
[1] 0.1086351

Results and Interpretation

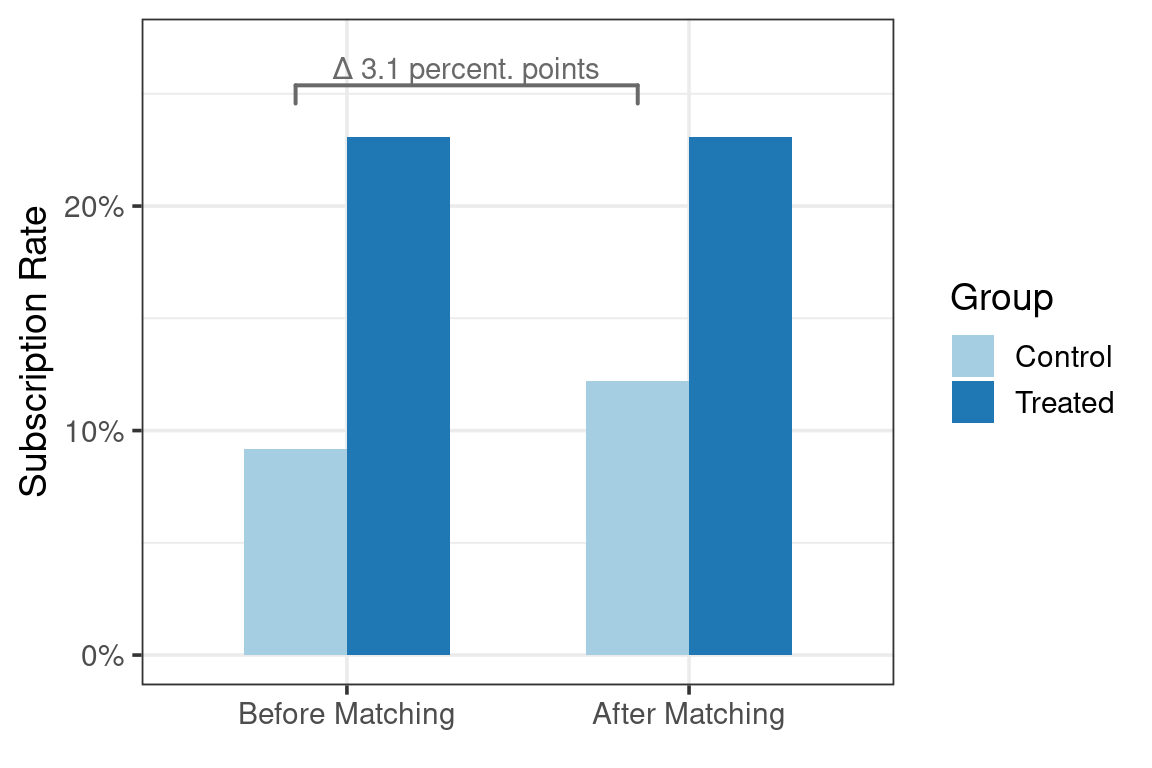
Before matching, customers who were previously contacted were \(13.91\) percentage points more likely to subscribe to a term deposit. After controlling for demographics and financial variables via propensity score matching, previously contacted customers were \(10.86\) percentage points more likely to subscribe than comparable new customers (\(p = 1.3128662\times 10^{-75}\)), which is \(3.05\) percentage points (\(21.92\%\)) less than the initial estimate.

  • Before matching: previously contacted customers have a much higher subscription rate.

  • After matching: the difference decreases, indicating that part of the initial gap was due to selection bias.

Figure 7: Subscription rates before and after matching.

Discussion and Limitations

Unobserved confounding: we only matched on observed variables; factors like personality or spending habits might still bias the result.

Choice of treatment: we assumed “previous contact” is the cause; other definitions (e.g., contact channel, number of calls) could be explored.

Generalization: results apply to customers similar to those treated (ATT), not necessarily to all clients.

Conclusion

In this tutorial, we’ve demonstrated how to estimate a causal effect using Propensity Score Matching with real marketing data.

The key takeaways:

  • PSM helps approximate experimental conditions in observational settings.

  • Always check covariate balance before interpreting results.

  • Proper treatment and covariate definitions are critical.

The full R code can be easily adapted to other business questions, for example, measuring the effect of marketing emails, app notifications, or loyalty programs when randomization is not possible.

References

Ho D, Imai K, King G, Stuart E (2011). “MatchIt: Nonparametric Preprocessing for Parametric Causal Inference.” Journal of Statistical Software, 42(8), 1-28. doi:10.18637/jss.v042.i08 https://doi.org/10.18637/jss.v042.i08.